A majority system of voting and counting called preferential voting is used to elect members of the House of Assembly. Preferential voting was first introduced in South Australia in 1929.
In order to win a seat in the House of Assembly, a candidate is required to obtain an absolute majority (more than 50%) of the total formal votes cast in an electoral district.
If a candidate has a majority of the votes, the candidate is elected and no further counting is necessary. If no candidate receives the majority, the candidate with the least number of formal votes is ‘excluded‘ and that candidate's ballot papers are re-sorted to the other candidates according to the second preference shown on each ballot paper. The process of exclusions is repeated until one candidate gains more than half of the formal votes and is elected.
Each count continues until only 2 candidates remain, regardless of whether a candidate gains an absolute majority earlier in the count.
If in the final count 2 candidates have an equal number of votes, the matter is referred by the Electoral Commissioner to the Court of Disputed Returns where the Court may determine the validity of disputed ballot papers. If it then appears that the deadlock has been resolved, the Court must declare the appropriate candidate elected, if not, the Court must order a fresh election.
An example of how preferences work in the House of Assembly
Kate, Lyn, Tom and Steve stand for election.
They receive the following formal first preference votes:
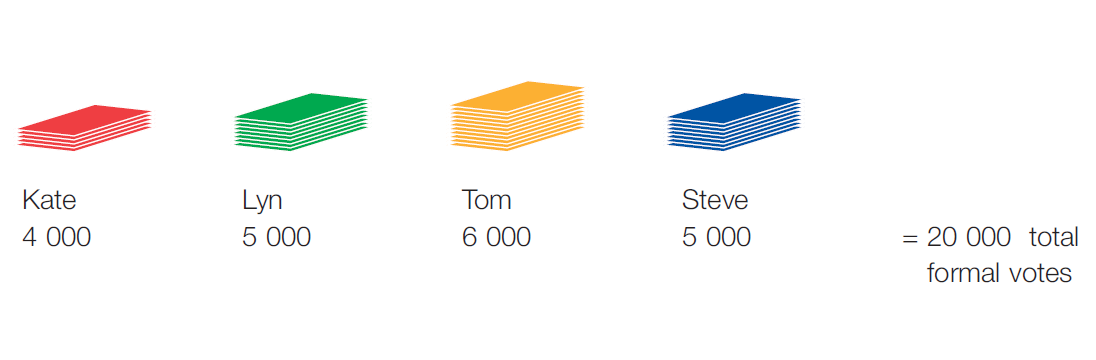
There are a total of 20,000 formal votes.
To be elected a candidate needs an absolute majority (more than 50% - or more than half of the vote)
As none of the candidates has gained an absolute majority of the votes (more than 10,000) at this first count, the candidate with the least number of votes (Kate) is excluded and her ballot papers are transferred to the other candidates according to which candidate was allocated the number 2 (second preference).
Kate’s votes are transferred as follows:
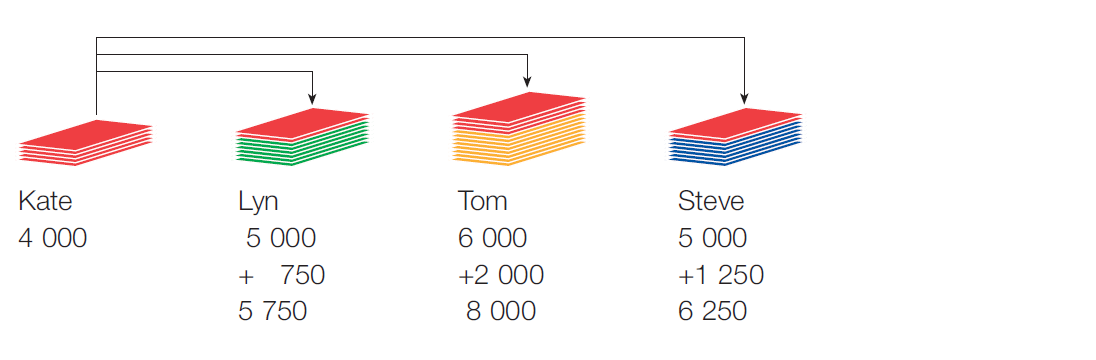
After Kate’s ballot papers have been distributed, neither Lyn, Tom, or Steve have gained an absolute majority. Lyn is now the candidate with the least number of votes so she is excluded and her ballot papers are distributed according to who was marked as the number ‘2’ (or the number ‘3’, if the ballot paper was previously transferred from Kate) preference.
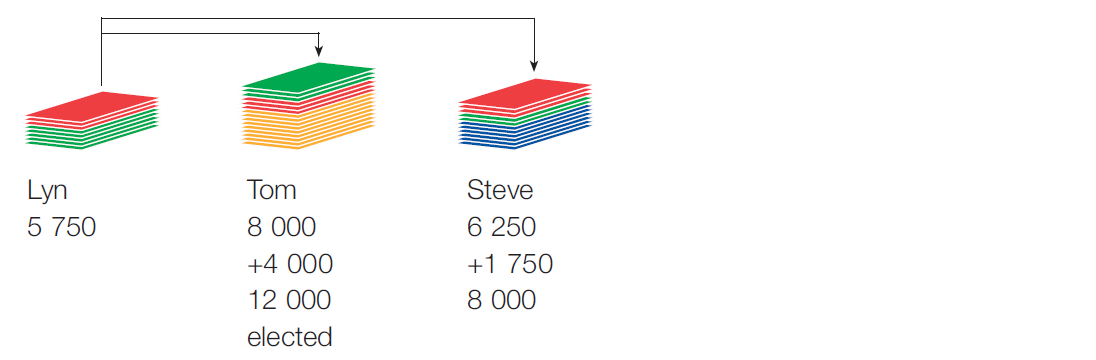
Once the preferences on Lyn’s ballot papers have been distributed (4,000 are marked for Tom and 1,750 for Steve) the ballot papers are totalled for each remaining candidate.
Tom now has more than half of the total votes cast (an absolute majority) and is declared the elected candidate.
